
设计仪器仪表时,总希望得到线性的输入输出关系,这样不仅可以使显示、记录刻度均匀、读数清楚、方便,而且能位仪器仪表在整个测量范围的灵敏度一致,量程比扩大。实际上,很多变量与测量转换所获得的电信号(往往因传感器的特性是非线性的)都呈非线性关系。例如热电偶在测温中产生的毫伏信号与温度之间为非线性关系,纸浆浓度变送器在测量中输出的电流信号与纸浆浓度之间是非线性关系,等等。
为了最后获得输入输出之间的线
性关系,模拟式仪器仪表不得不采用校正机构或线性化电路对测量特性进行补偿校正。这些硬件补偿措施的效果不可能很好,却增加了成本,降低了可靠性。微机化仪器仪表充分利用微机的运算能力,通过测量算法进行非线性校正,而不需要任何硬件补偿装置,与硬件补偿方法比较,既可大大提高精度,又能降低成本,提高可靠性。线性化算法的关键在找到一合适的校正函数。根据对传感器特性的标定情况,线性化方法可有曲线拟合、插值、查表以及本章第一节讲到的非线性标度变换等多种方法,后者仅适用于非线性关系可用数学公式确切描述的情况。
一、连续函数拟合法
此方法的目标是用一个确定的解析函数来拟合所得标定曲线(校准曲线)、包括确定该函数的类型、具体结构形式及其一切必要的参数,然后通过函数的数值计算求得准确的测量结
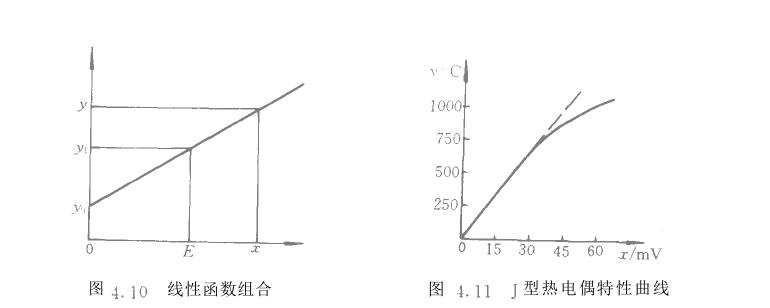
二、插值法(分段拟合法)
插恒法又称分段拟合法,它把校准曲线的整个区间划分成若干段,每段用根据输入量x所在的区段,即可按该段的拟台多项式计算出准确的测量结果。插值法通常有线性插值和抛物线插恒等两种形式。
1.线性插恒法
相邻分段点之间用直线相连,以代替相应的曲线段。实现线性插值的步骤如下:
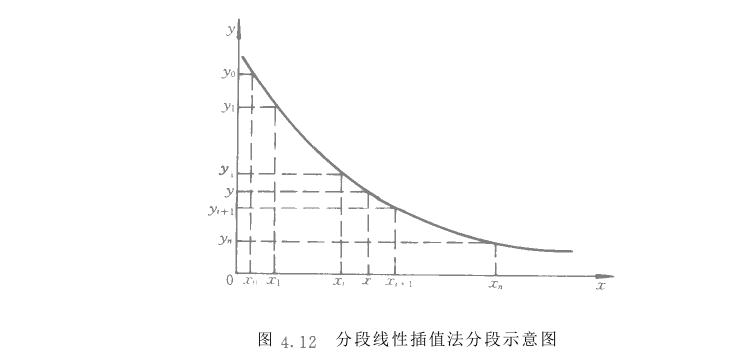
①将校准曲线进行分段,选取各插恒基点。为了使基点的选取更合理,可根据不同的曲线用不同的方法分段。等距分段法是较常用的方法。该方法沿:轴等距离地选取插恒基点,这样计算简单易行。但是当函数的曲率和斜率变化较大时,往往会产生一定误差。为了减小误差,必须把基点分得很细,这样势必占用较多内存,并使计算时间变长。非等距分段可根据函数曲线形状的变化率修正插值间的距离,也可以使常用测量范围插恒距离小一点,而使不常用区域的插值距离大一些。非等距插恒点的选取和计算比较麻烦。
②确定各插恒点x值,计算u值,拟合直线段的斜率6.恒,全部按一定规律存放在存储器中。以上两步骤在设计微机化仪器仪表中完成。仪器仪表工作后完成以下几步。
2.抛物线插恒法
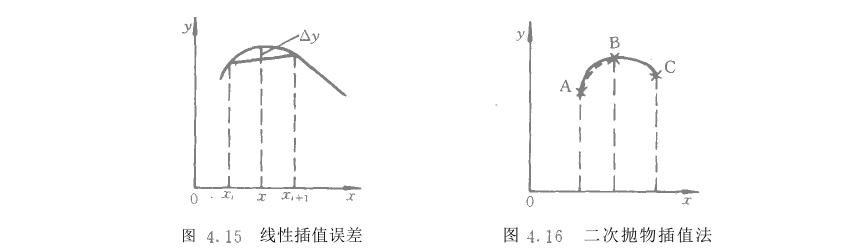
线性插恒过能解抉绝大多数非线性校正问题。仍然有一些特殊情况要另外考虑。如图4。15所示,当传感器校淮曲线某部分很弯时,如仍用线性插值法,有可能出现两插点之间的曲线也很弯的现象,这样插值的结果将产生很大的误差A小当Av大于所允许的误差时,线性插恒过即告失败。增加插值基点的数量,缩小两相邻插值点的距离可以减小误差,但插值点太多势必会占用较多内存单元,且使计算时间增长,整个工作速度降低。为了解抉这个问题,人们采用了一种称为二次抛物线插值法的方法来取代线性插值法。
三、查表法
无论连续函数拟合法还是插值法线性化,都需要在线校正过程中进行相当多工作量的、甚至是复杂的计算。苔计算中处理不当字节数不够等k就可能造成计算误差,计算必然使得程序变长,处理速度降低。而查表法可以避开处理计算,以较高的精度和较快的速度进行线性处理。查表法要求事先用表格形式确定采样结果与被测量之间关系,并将表格按一定方法(例如大小顺序)存入内存单元。处理过程中先取得测量结果,然后查表得到被测量真值。
较简单的表格形式是清单。把一列无序数据依次存入内存一些相连的存储单元中,就成为一张清单。存储地址可以任意选取,不过应以某种方式记住,以便以后检索。例如,可以把清单首地址存入某一指定的存储单元中,检索时再从这儿取得清单首址。

如果用连续转换的整数作为偏移量,加上表格首址,就可以直接从表格中取到待查找变量数值,当被测量用多字节表示时,可将转换结果乘上字节数后作为偏移量。
如果数据采集的结果要经过其它变换处理(例如标度变换)后才能用以查表,则应建立两个表格,一个表格中放测量变换结果f,另一个映像表中放待查找变量vP4安排两个表的首址之间的相差偏移量。当从x表中查到对应于测量结果的数据后,其地址加上相差偏移量,即可查找到被测变量。(本文来源:正航仪器设备有限公司)http://www.zhushanzz.com

 粤公网安备 44190002001229号
粤公网安备 44190002001229号